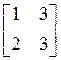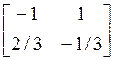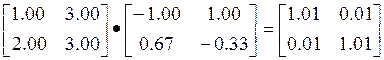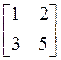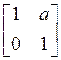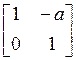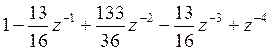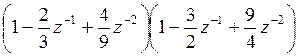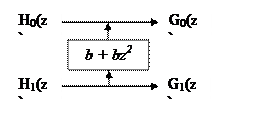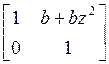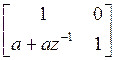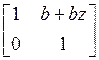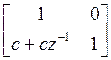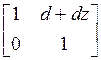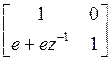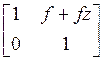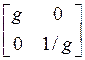|
Structurally Linear Phase Factorization of Filterbanks
Perfect Reconstruction: It is desirable for a filterbank to be perfect reconstruction (PR), such that its exact inverse exists. For example, take a matrix
It’s exact inverse is
So this matrix is PR. Structural Property: A property is structurally imposed, if it is valid even with change of values. We need to change values in two cases. First one is implementation. Let us implement the above example matrix and its inverse using any finite precision system, say, upto 2 decimal digits. Then we have a problem, since
and the matrix is no longer PR. So, this matrix is PR, but not structurally PR. Some matrices are structurally PR. Try
Second case when we need to change the values is during design (of a filterbank). We can write such matrices using variables. Can a matrix with some variable entries be structurally PR? Yes. For example, inverse of
is
Assuming that any change in a is also reflected in −a, the inverse is always exact. Linear Phase: It is sometimes desirable for a filterbank to be linear phase (LP), such that the filter coefficients are symmetric/antisymmetric. Is LP a structural property? In direct from it is. However, we design as well as implement filterbanks using factorization, or in cascade form. Then LP is not a structural property. For example, an LP filter
may be factorized as
If one decimal digit finite precision is used for each coefficient, then
the resulting filter
Structurally LP and PR Factorization: Given any LP PR filterbank with two filters H0(z), H1(z), we show that we can always obtain another LP PR filterbank with two smaller-length filters G0(z), G1(z), using a lifting matrix
as shown in the next figure. Repeated application of this principle results in a complete factorization and design of all such filterbanks. Example: A known LP PR filterbank used in wavelet based image compression has filters H0(z) = [-0.0085, 0.0038, 0.0473, -0.0335, -0.0689, 0.3833, 0.7672, 0.3833, -0.0689, -0.0335, 0.0473, 0.0038, -0.0085], H1(z) = [-0.0142, 0.0063, 0.1097, -0.0692, -0.4481, 0.8328, -0.4481, -0.0692, 0.1097, 0.0063, -0.0142]. Its polyphase matrix is factorized to
where a=0.5974, b=1.5402, c=0.1106, d=-0.1904, e=-0.1972, f=-2.1813, g=1.0165.
|