|
Data-driven sciences are widely
regarded as the fourth paradigm of sciences that will fundamentally change
the society and our everyday lives. Indeed, artificial intelligence (AI) models
have already revolutionized and transformed various data-intensive industries. Machine learning and deep learning models have
achieved unprecedented extraordinary performance for image, text, audio, video,
and network data analysis. The great successes are mainly due to three reasons,
i.e., accumulation of the gigantic amount of data, ever-increasing
computational power, and design of the highly efficient algorithms. Further, the
remarkable achievement of AlphaFold2 for
protein folding problem has ushered in a new era for AI-based molecular
data analysis for materials, chemistry, and biology.
With the excitement and
opportunities come challenges. Currently, one of the central challenges for
AI-based molecular data analysis is molecular representation, which is to identify
or design appropriate molecular descriptors or fingerprints. Proper descriptors
should preserve the most important and intrinsic molecular properties and
information that directly determinate molecular functions. In this way, they
can be better “understood” by machine learning models. In fact, the performance
of many learning methods is heavily dependent on the choice of data
representation and featurization, which is a long-standing issue for cheminformatics
and bioinformatics. Traditional
molecular descriptors are properties obtained from structural geometry/topology,
chemical conformation, chemical graph, as well as molecular formula,
hydrophobicity, steric properties, and electronic properties. These descriptors
are widely used in the quantitative structure-activity relationship (QSAR) and
learning models.
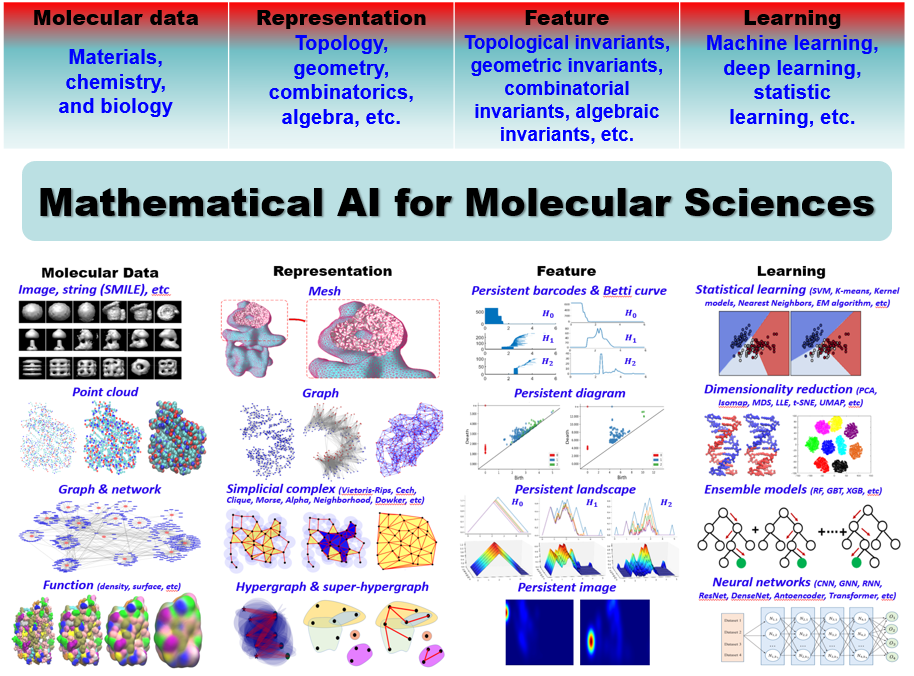
Mathematical AI for Molecular Sciences
is proposed for molecular representation, featurization, and learning. As
illustrated above, various types of data, in particular, molecular data from materials,
chemistry, and biology, can be represented using topological models, including graphs,
simplicial complexes, hypergraphs, etc. From these representations, various
mathematical invariants are obtained by using advance mathematical models from algebraic
topology, discrete geometry, combinatorics, etc. These mathematical invariants are
used as input features for learning models. Dramatically different from
previous models, molecular data are modelled using higher-dimensional
topologies, such as simplicial complexes and hypergraphs, and
filtration-induced multiscale representations. Further, mathematical
invariant-based features characterize the most intrinsic and fundamental
properties and have a better transferability for learning models.
A brief introduction of the area can be found in 2021 winter school lectures at Dalian, AATRN talk, report in Chinese for the series of talks on "Math for AI & AI for math", and Prof.Guowei Wei's works (SIAM news, Harvard talk, D3R news). We
sincerely welcome highly motivated students
and postdocs to join our group!
*New* IA matemática para ciencias moleculares, Spanish translation by Chicks Gold.
*New* Matematička Ai Za Molekularne Znanosti, Croatian translation by Chicks Gold.
|
- Persistent Spectral based machine learning (PerSpect ML) for drug design
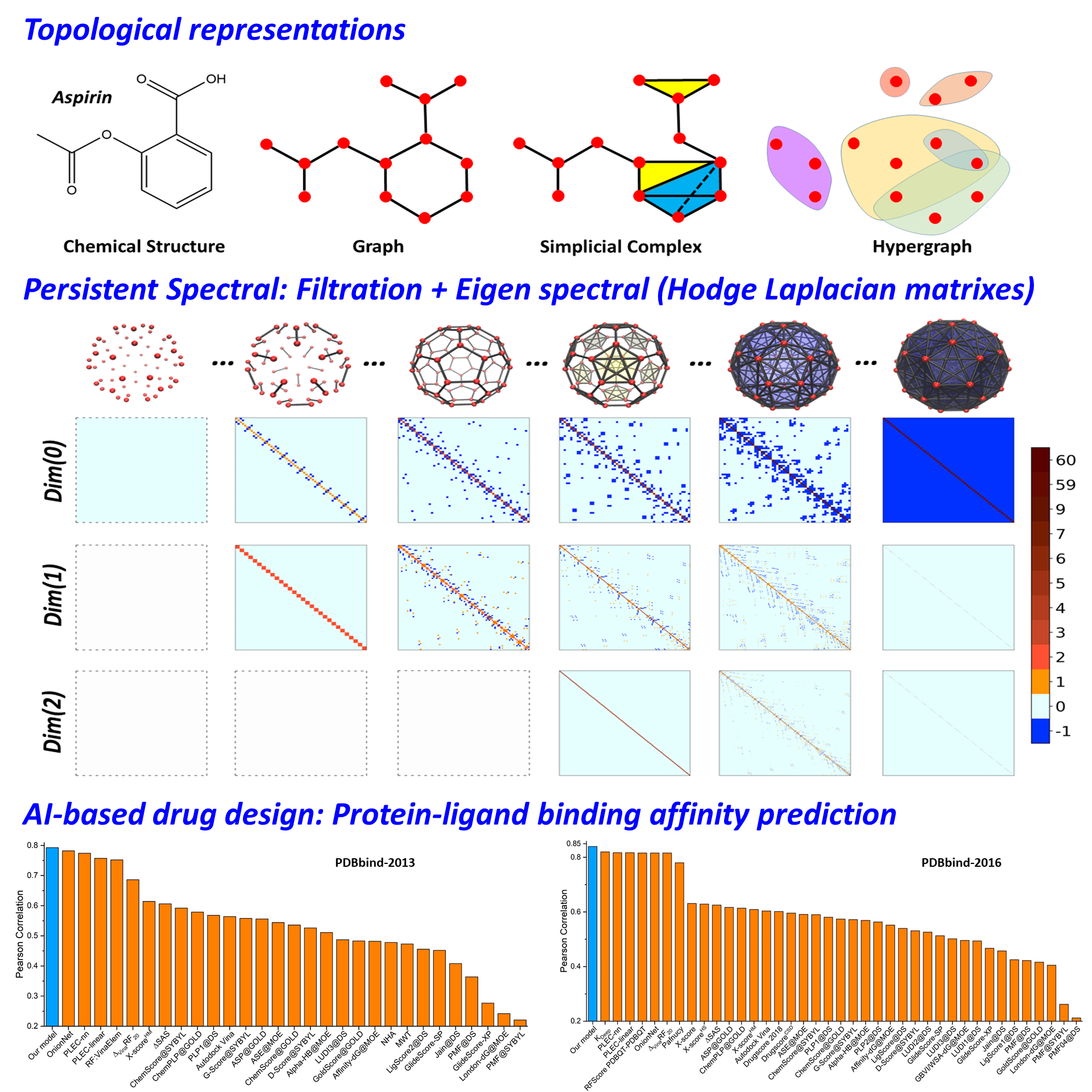 |
The structure-function relationship is of essential importance
to the analysis of biomolecular flexibility, dynamics, interactions, and functions.
Topology studies the network and connection information within the data and
provides an effective way of structure characterization. As illustrated in the
figures, there are three basic topological representations, including graph,
simplicial complex, and hypergraph, for molecular structures. Features for learning models can be obtained
from these representations. The essential idea is to use eigen-spectrum-based properties
as molecular descriptors.
Our persistent spectral (PerSpect) theory covers three
basic models, i.e., PerSpect graph, PerSpect simplicial complex, and PerSpect
hypergraph. These models are filtration-based multidimensional spectral methods.
Mathematically, spectral graph theory, spectral simplicial complex, and
spectral hypergraph have been developed based on graph, simplicial complex, and
hypergraph. These models use different types of connection matrixes, in
particular, Hodge (combinatorial) Laplacian matrixes, to represent structure
connection. The multidimensional representation is achieved through a filtration
process. The persistence and variation of eigen spectrum information during the
filtration process are characterized by persistent functions or attributes,
which are further used as molecular
features or fingerprints.
Reference: Zhenyu Meng and Kelin Xia, "Persistent spectral based machine learning
(PerSpect ML) for protein-ligand binding affinity prediction", Science
advances (2021)
|
- Persistent Ricci curvature based machine learning
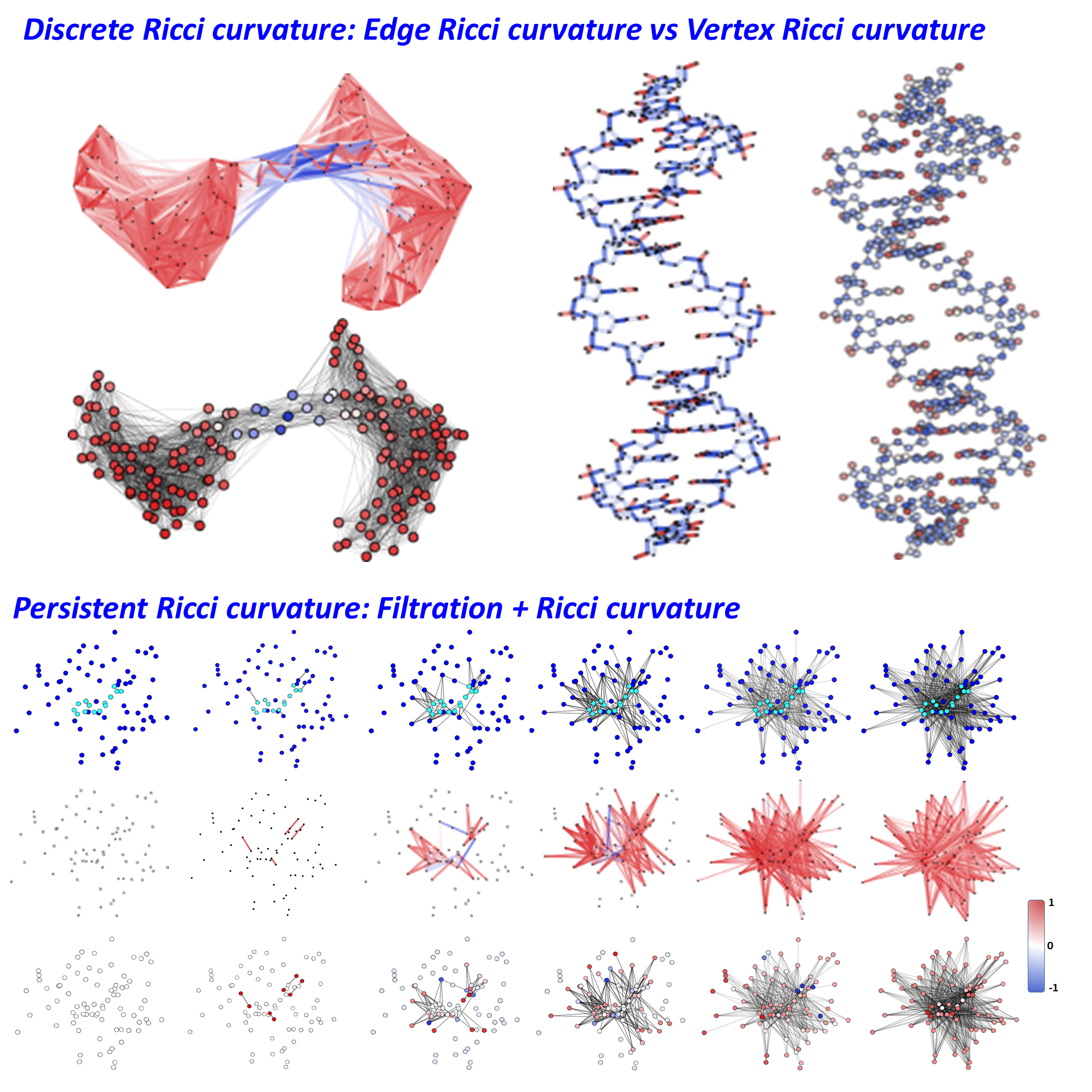 |
Ricci curvature is one of the fundamental concepts in differential
geometry and theoretical physic. Two discrete Ricci curvature forms, i.e.,
Ollivier Ricci curvature (ORC) and Forman Ricci curvature (FRC), have been
developed to characterize different aspects of the classical Ricci curvature.
ORC is defined as the Wasserstein distance between two associated probability
measurements on metric spaces. It captures clustering and coherence properties
of global and local structures in networks. In contrast, FRC is defined as a combinatorial
property of upper adjacent, lower-adjacent and parallel simplexes on CW
complexes. This combinatorial curvature can be directly derived from the
combinatorial Bochner-Weitzenbock decomposition. It characterizes geodesics
dispersal property and algebraic topological information within networks. Even
though the two discrete forms can have totally different values, sometimes even
signs, for network substructures, they are found to be highly correlated in
various complex networks. Generally speaking, positive ORCs or FRCs are
commonly found in densely-packed clusters or “communities”, while negative ORCs
or FRCs usually represent bridges or links between clusters.
The persistent Ricci curvature is proposed to combine
filtration-based multiscale representations with Ricci curvatures for molecular
featurization. Ricci curvatures are systematically evaluated on all the
graphs/simplicial complexes/hypergraphs in the filtration process. The
statistical and combinatorial properties of Ricci curvatures during the
filtration are used as molecular descriptors.
Referece: JunJie Wee and Kelin Xia, "Forman persistent Ricci curvature (FPRC)
based machine learning models for protein–ligand binding affinity
prediction", Briefings In Bioinformatics (2021)
JunJie Wee and Kelin Xia, "Ollivier persistent Ricci curvature
(OPRC) based machine learning for protein-ligand binding affinity
prediction", Journal of Chemical Information and Modeling, https://doi.org/10.1021/acs.jcim.0c01415 (2021)
|
- Peristent hypergraph based machine learning
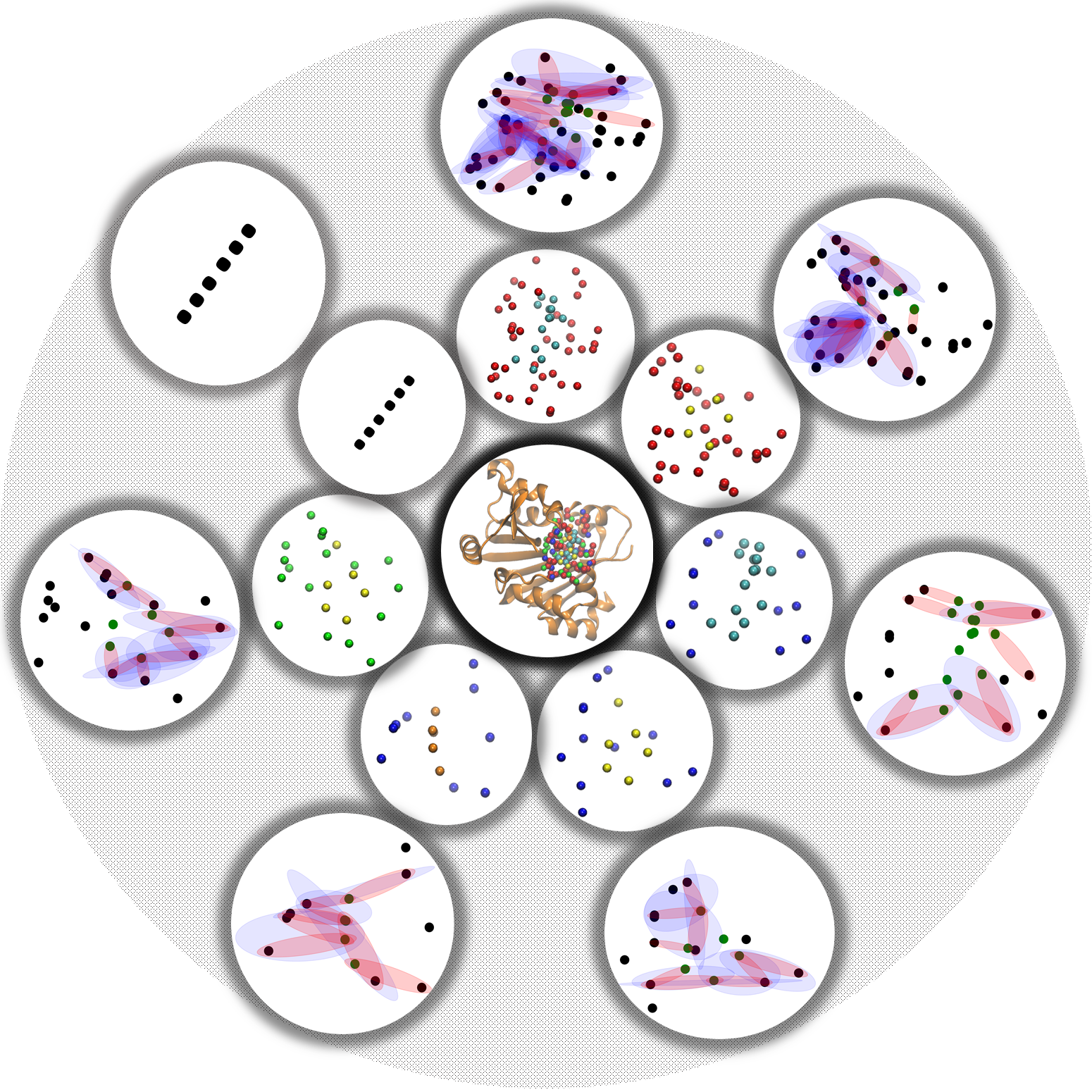 | Hypergraphs
are powerful topological representations that can characterize more
general structure information than graphs and simplicial complexes. A
hypergraph is composed of hyperedges, which are sets of vertices.
Essentially, a hyperedge can be viewed as a generalization of simplexes
without the closeness under boundary conditions. The interactions
between molecules at atomic level can be well represented as
hypergraphs. Mathematically, a hyperedge can be defined a set of
vertices (atoms) that have at least one from each molecules. For
instance, in protein-ligand interactions, a hyperedge is defined among
protein and ligand atoms, but it has at least one atom from protein and
the other from ligand. In this way, hyperedges represent (many-boday)
interactions between protein and ligand atoms.
Element-specific models are widely used to decompose molecular
complexes into a series of atom specific combinations. More
specifically, proteins can be decomposed into at least 5 types of atom
sets, i.e., C, O, N, S, and H, while ligand usually have at least 10
types of atom, including C, N, O, S, P, F, Cl, Br, I and H. In this
way, upto 50 atom combinations can be obtained and the corresponding
hypergraphs can be constructed. Topological and geometric invariants
can be systematically obtained from these hyperedges and further used
as features for machine learning models.
Reference:
Xiang Liu, Huitao Feng, Jie Wu, and Kelin Xia, "Persistent spectral
hypergraph based machine learning (PSH-ML) for protein-ligand binding
affinity prediction", Briefings In Bioinformatics (2021)
Xiang Liu, Xiangjun Wang, Jie Wu, and Kelin Xia, "Hypergraph based
persistent cohomology (HPC) for molecular representations in drug
design", Briefings In Bioinformatics (2021)
|
Geometric and Variational modeling
- Variational
multi-scale models
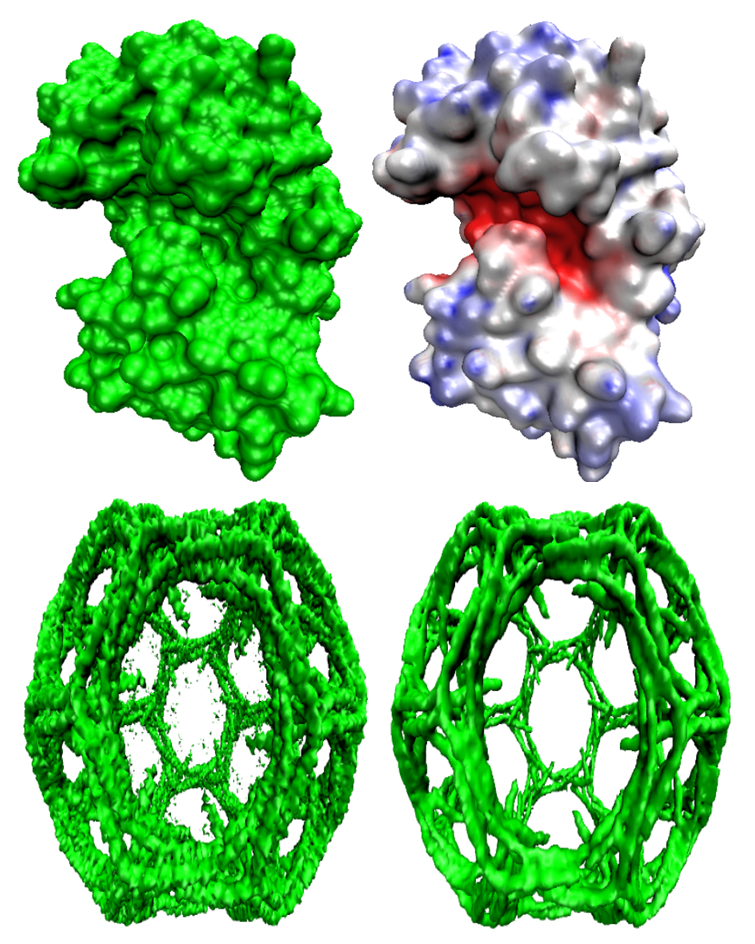 |
We
develop geometric modeling and computational algorithm for biomolecular
structures from two data sources: Protein Data Bank (PDB) and Electron
Microscopy Data Bank (EMDB) in the Eulerian (or Cartesian)
representation. Molecular surface (MS) contains non-smooth geometric
singularities, such as cusps, tips and selfintersecting facets, which
often lead to computational instabilities in molecular simulations, and
violate the physical principle of surface free energy minimization.
Variational multiscale surface definitions are proposed based on
geometric flows and solvation analysis of biomolecular systems. The
resulting surfaces are free of geometric singularities and minimize the
total free energy of the biomolecular system. High order partial
differential equation (PDE)-based nonlinear filters are employed for
EMDB data processing. After the construction of protein
multiresolution surfaces, we explore the analysis and characterization
of surface morphology by the consideration of Gaussian curvature, mean
curvature, maximum curvature, minimum curvature, shape index, and
curvedness. Based on the curvature and electrostatic analysis from our
multiresolution surfaces, we introduce a new concept, the polarized
curvature, for the prediction of protein binding sites.
|
- Protein flexibility
and rigidity analysis
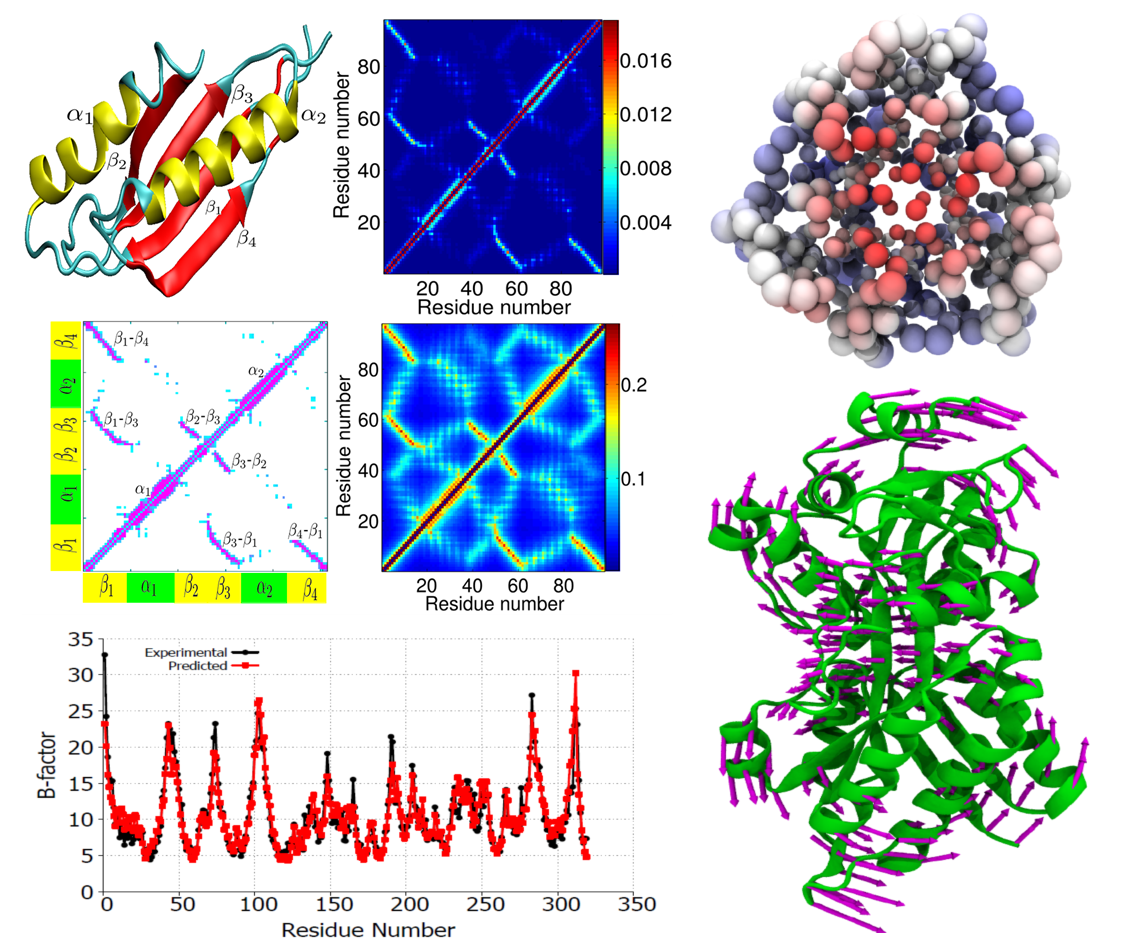 |
Protein
structural fluctuation, typically measured by Debye-Waller factors, or
B-factors, is a manifestation of protein flexibility, which strongly
correlates to protein function. The flexibility-rigidity index (FRI) is
a newly proposed method for the construction of atomic rigidity
functions required in the theory of continuum elasticity with atomic
rigidity, which is a new multiscale formalism for describing
excessively large biomolecular systems. The FRI method analyzes protein
rigidity and flexibility and is capable of predicting protein B-factors
without resorting to matrix diagonalization. A fundamental assumption
used in the FRI is that protein structures are uniquely determined by
various internal and external interactions, while the protein
functions, such as stability and flexibility, are solely determined by
the structure. As such, one can predict protein flexibility without
resorting to the protein interaction Hamiltonian. Additionally, we
propose anisotropic FRI (aFRI) algorithms for the analysis of protein
collective dynamics. Eigenvectors obtained from the proposed aFRI
algorithms are able to demonstrate collective motions.
|
Scientific Computing
- MIB method for
multi-material interface problem
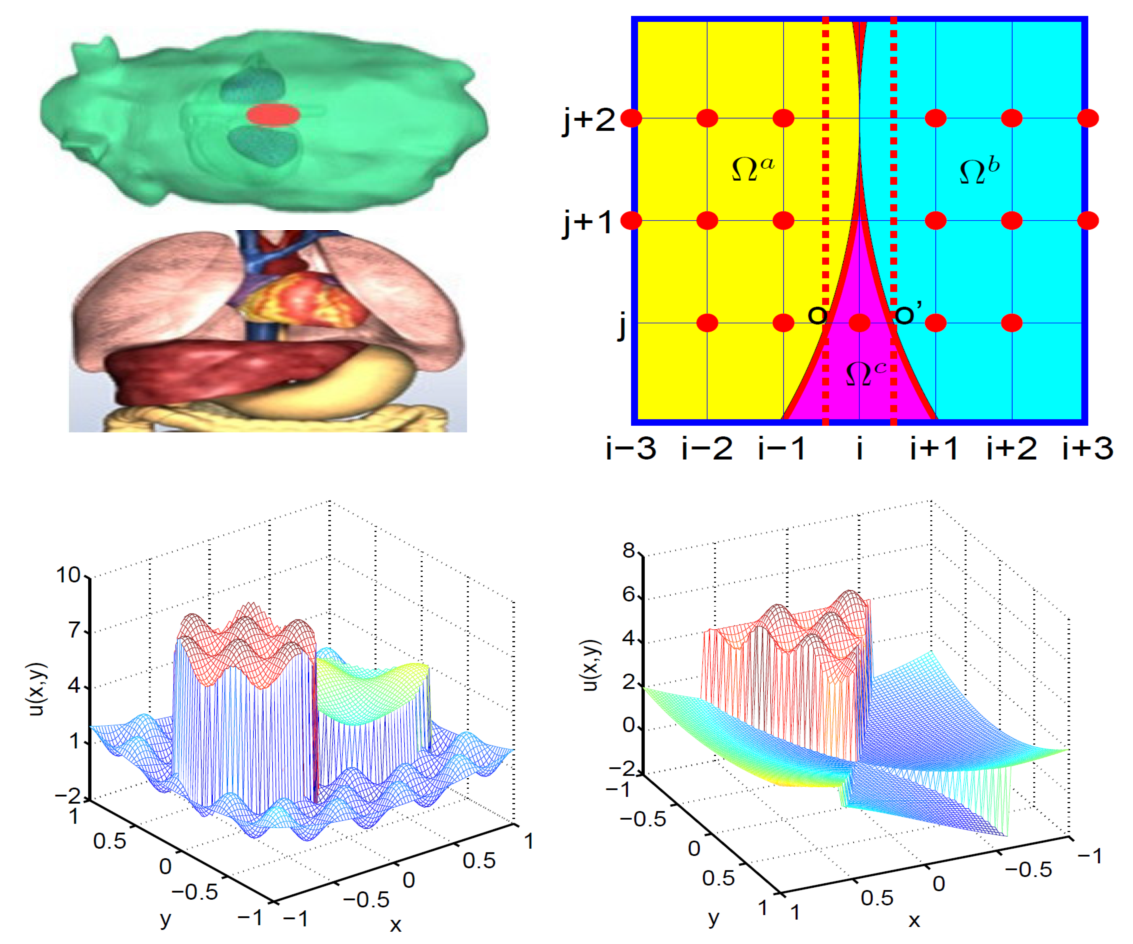 |
Multi-material
interface problems are omnipresent in science, engineering and daily
life. The solution to this class of problems becomes exceptionally
challenging when more than two heterogeneous materials join at one
point of the space and form a geometric singularityprimary. Based on
the MIB method, several schemes have been constructed to solve 2D
elliptic equations with discontinuous coefficients associated with
three-material interfaces. The essential idea is to smoothly
extend functions across the interface and employ the
fictitious values at irregular points. For the
geometric singularities, two sets of interface conditions are
considered simultaneously. Intensive
numerical experiments are carried out to validate the proposed schemes.
A second order of accuracy is obtained for complex geometric and
geometric singularities.
|
- Adaptive mesh based MIB method
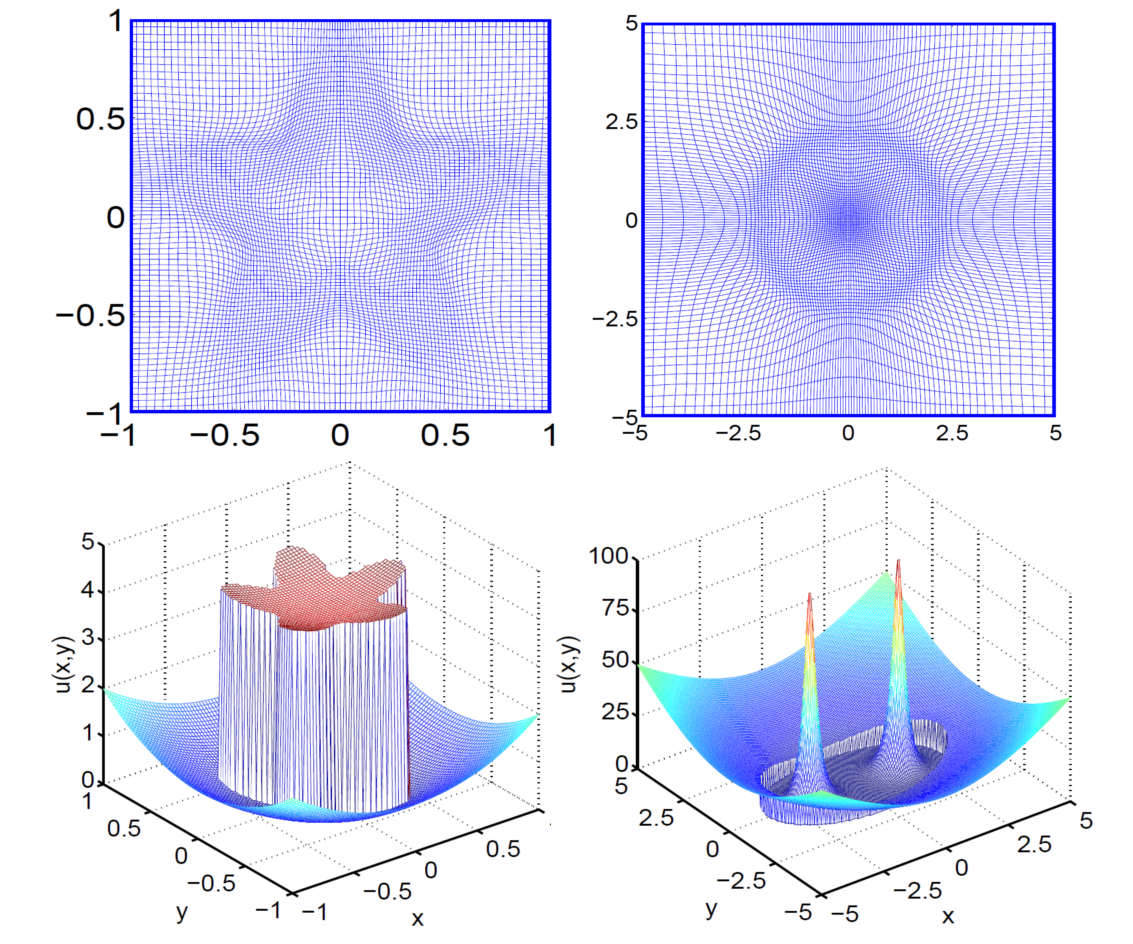 |
Mesh
deformation methods break down for elliptic PDEs interface
problems, as additional interface jump conditions are required to
maintain the well-posedness of the governing equation. An
interface technique based adaptively deformed mesh strategy is
introduced for resolving elliptic interface problems. We take
the
advantages of the high accuracy, flexibility and robustness
of MIB
method to construct an adaptively deformed mesh based interface method.
The proposed method generates deformed meshes in the physical domain
and solves the transformed governed equations in the computational
domain, which maintains regular Cartesian meshes. The mesh deformation
is realized by a mesh transformation PDE, which controls the mesh
redistribution by a source term. The source term consists of a monitor
function, which builds in mesh contraction rules. Both interface
geometry based deformed meshes and solution gradient based deformed
meshes are constructed to reduce errors in solving elliptic
interface problems. The proposed adaptively deformed mesh based
interface method is extensively validated by many numerical
experiments. Numerical results indicate that the adaptively deformed
mesh based interface method outperforms the original MIB method for
dealing with elliptic interface problems.
|
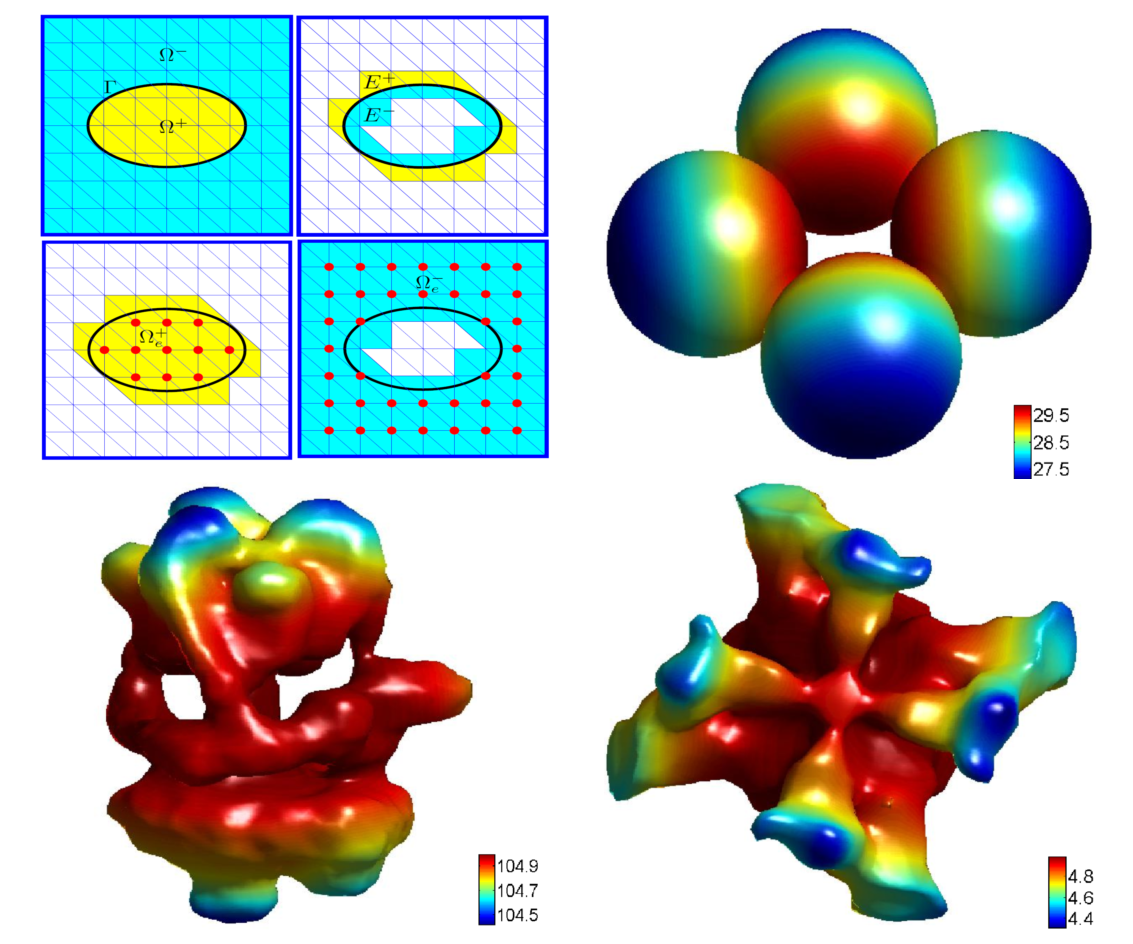 |
A
MIB Galerkin formulation is developped for solving the
elliptic
interface problem. In this approach, we build up two sets of elements
respectively on two extended subdomains which both include the
interface. As a result, two sets of elements overlap each other near
the interface. Fictitious solutions are defined on the overlapping part
of the elements, so that the differentiation operations of the original
PDEs can be discretized as if there was no interface. The extra
coeffients of polynomial basis functions, which furnish the overlapping
elements and solve the fictitious solutions, are determined by
interface jump conditions. Consequently, the interface jump conditions
are rigorously enforced on the interface. The present method utilizes
Cartesian meshes to avoid the mesh generation in conventional finite
element methods (FEMs). The accuracy, stability and robustness of the
proposed 3D MIB Galerkin are extensively validated. Near
second
order accuracy has been confirmed. To our knowledge, it is the first
time for an FEM to show a near second order convergence in solvingthe
Poisson equation with realistic protein surfaces. Additionally, the
present work offers the first known near second order accurate method
for C_1 continuous or H_2 continuous solutions associated with a
Lipschitz continuous interface.
|
|


