Biological Physics
The study of the morphology of living system is an area of active research that dates back to the seminal work “On Growth and Form” by D’Arcy Wentworth Thompson in 1917, which laid the foundation of applying concepts from mathematics and physics to understand the beautiful and complex forms observed in nature. My research focuses on understanding the morphology of biological system under different situations, most of which involve non-equilibrium processes, such as growth, change in external environmental conditions such as noise, applied stresses, humidity, etc. Most of the research in my group focuses on the study of individual organisms and we are starting to foray into the realm of the collective. We are interested in questions such as “What is their shape?”, “How are they formed?”, “What are emergent states?”. Through the study of different biological systems, we hope to extract general principles that can elucidate biological pattern and organization. Some notable projects by my group are listed below.
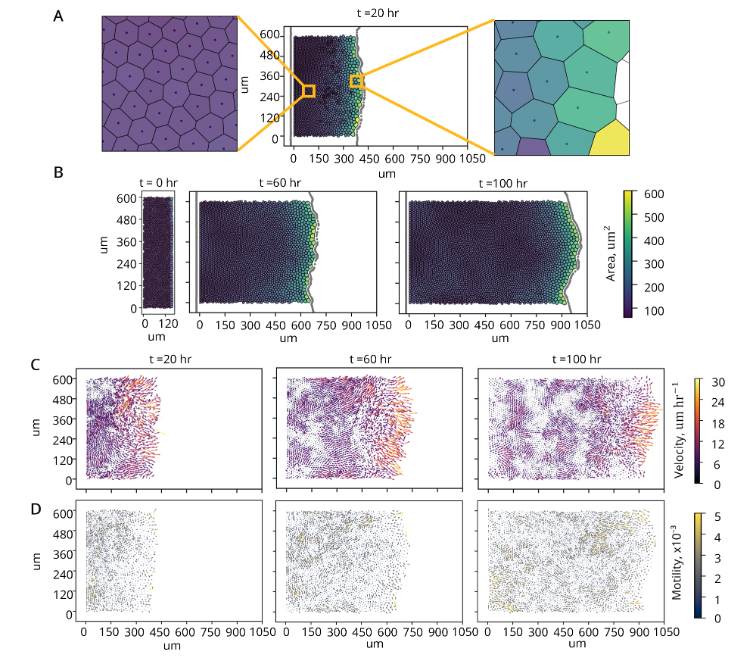
Hon Lin Too, Haiyi Liang, and Ee Hou Yong,
"Emergence of Distinct Cell Morphology and Size of Confluent Cell Sheet,"
forthcoming
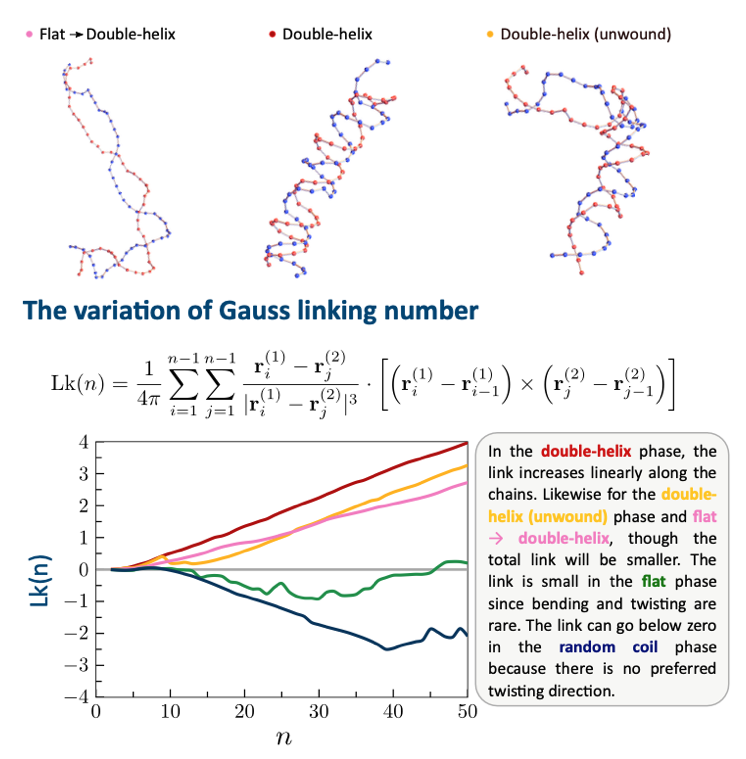
Farisan Dary, Haiyi Liang, and Ee Hou Yong,
"Helical stability of double-stranded semiflexible chains with interstrand interactions,"
forthcoming
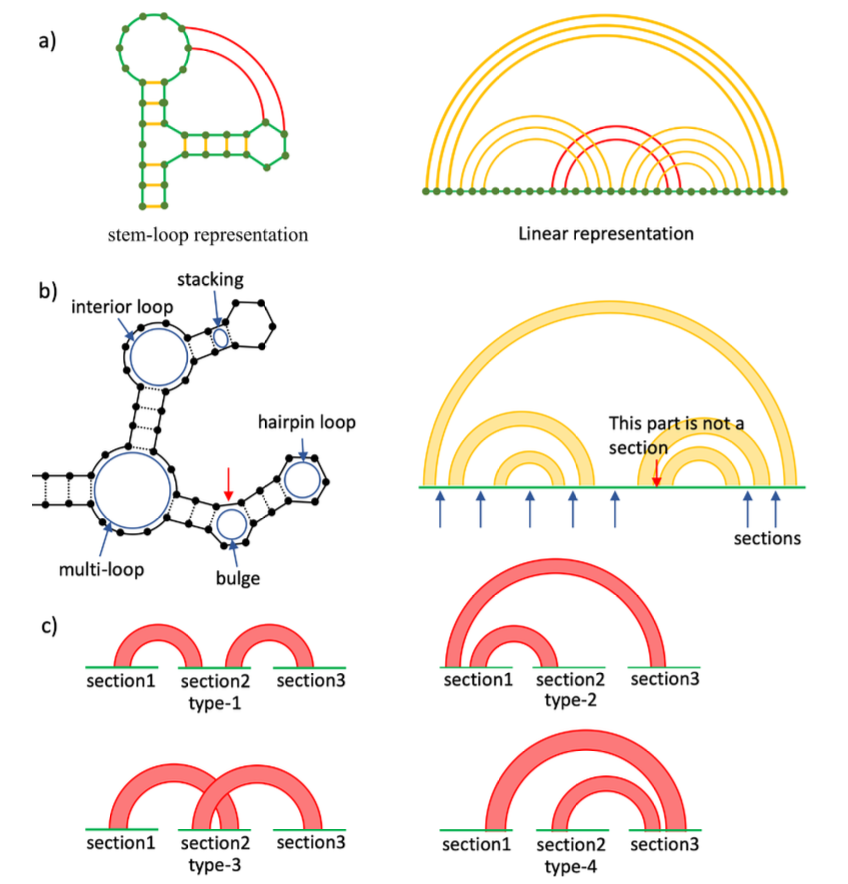
Ryota Masuki, Donn Liew, and Ee Hou Yong,
"Hierarchical Analysis of RNA Secondary Structures with Pseudoknots Based on Sections,"
forthcoming
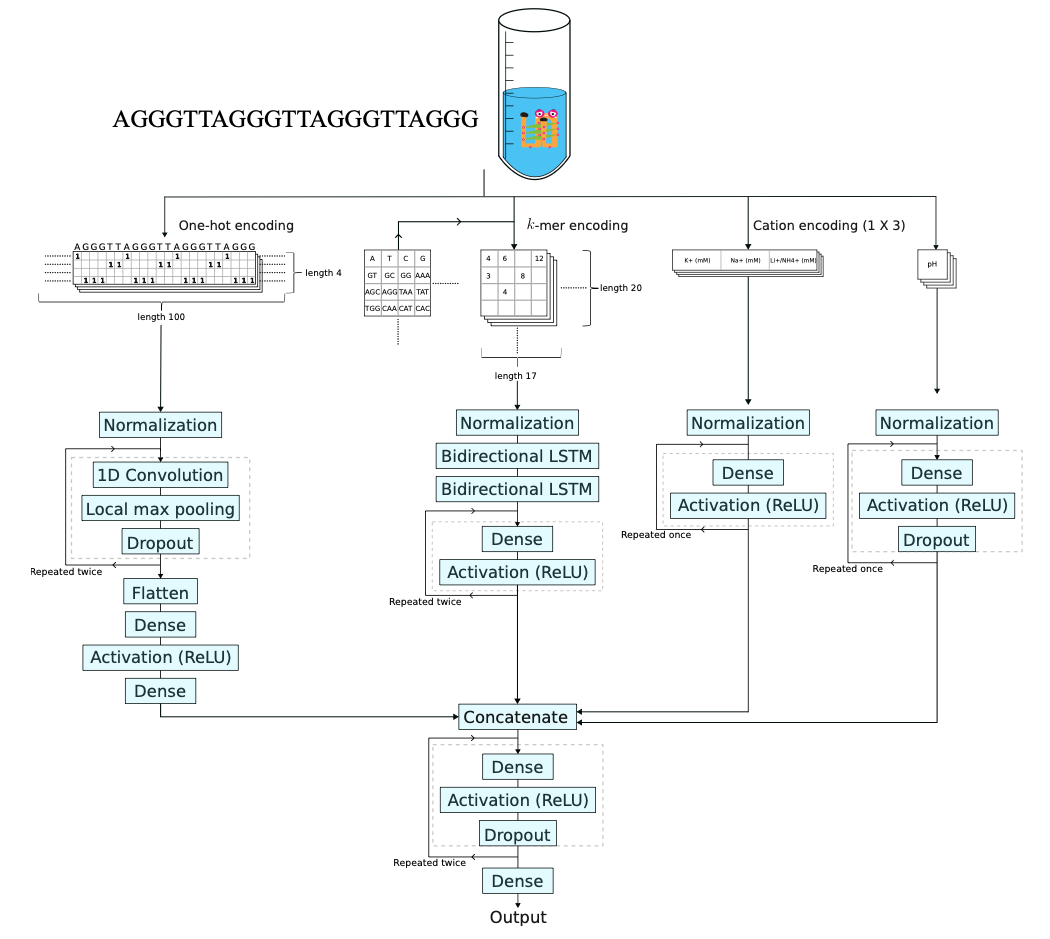
Donn Liew, Akesha Dinuli Dharmatilleke, Edwin See, and Ee Hou Yong,
"G4STAB: A multi-input deep learning model to predict G-quadruplex thermodynamic stability based on sequence and salt concentration ,"
Bioinformatics, btaf545
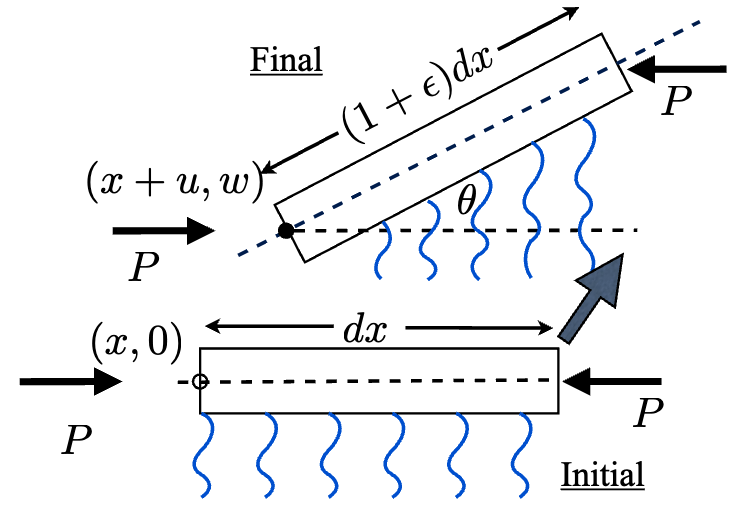
Ee Hou Yong and L. Mahadevan,
"Lyapunov-Schmidt bifurcation analysis of a supported compressible elastic beam,"
Nonlinearity 38, 085005, 2025.
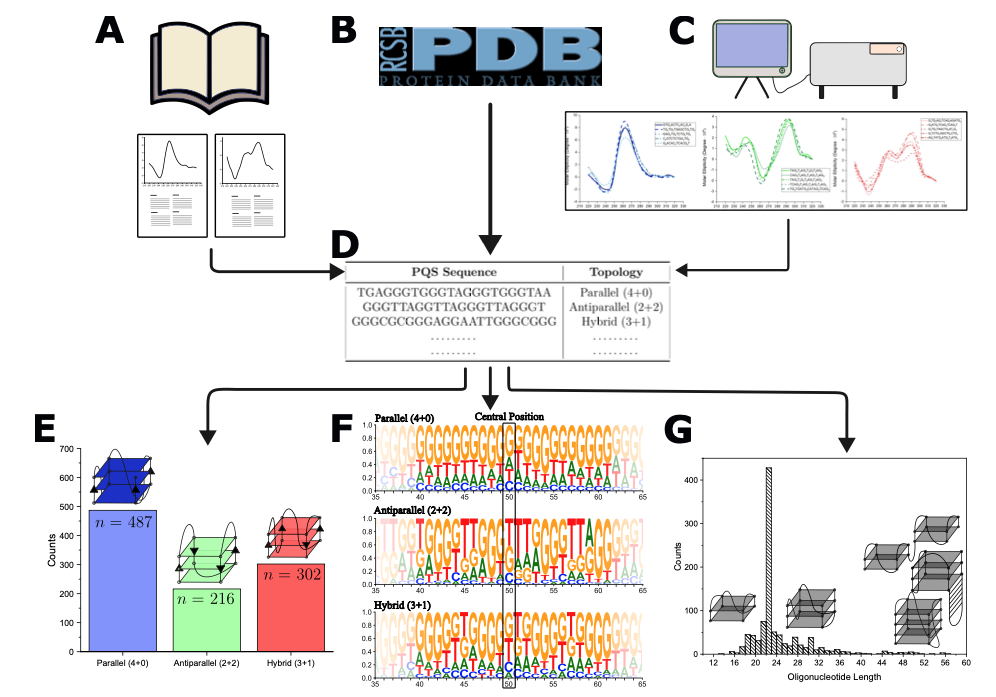
Donn Liew, Zi Way Lim, and Ee Hou Yong,
"Machine learning-based prediction of DNA G-quadruplex folding topology with G4ShapePredictor,"
Scientific Reports 14(1), 24238, 2024.
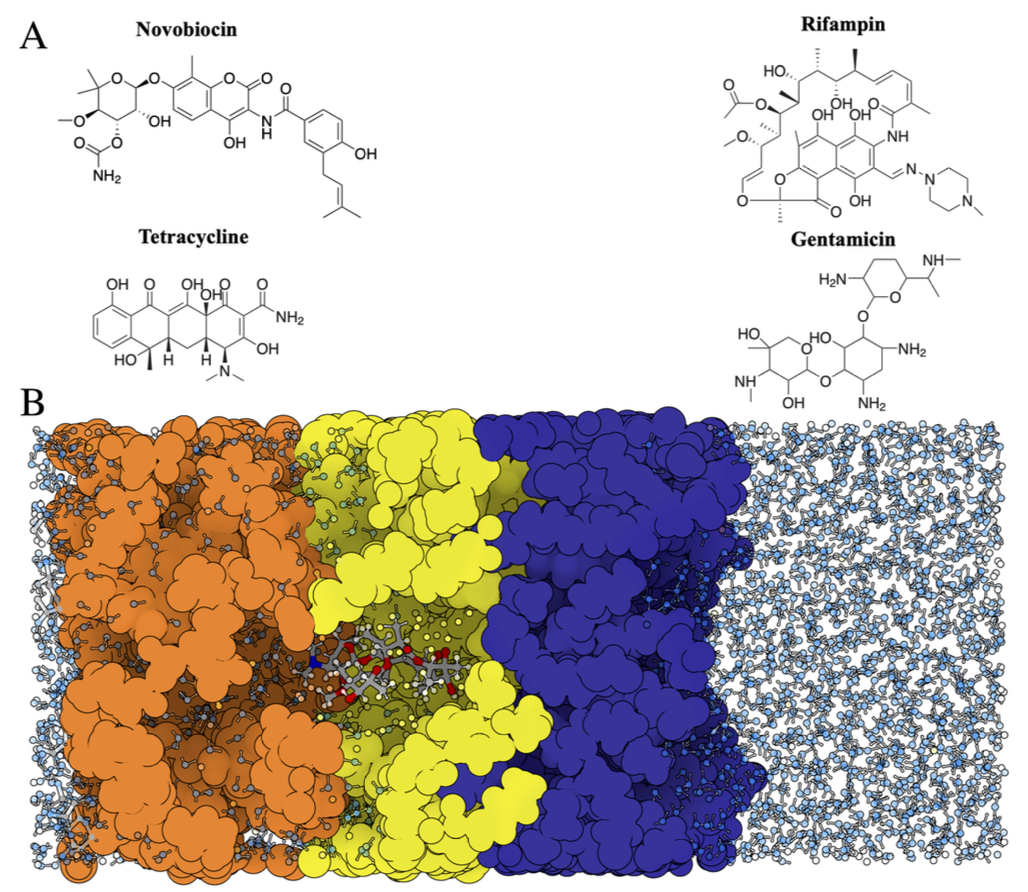
Javad Deylami, Shu Sin Chng, and Ee Hou Yong,
“Elucidating Antibiotic Permeation through the Escherichia coli Outer Membrane: Insights from Molecular Dynamics,”
Journal of Chemical Information and Modeling, 64(21), 8310, 2024.
Research covered in Nature Index article
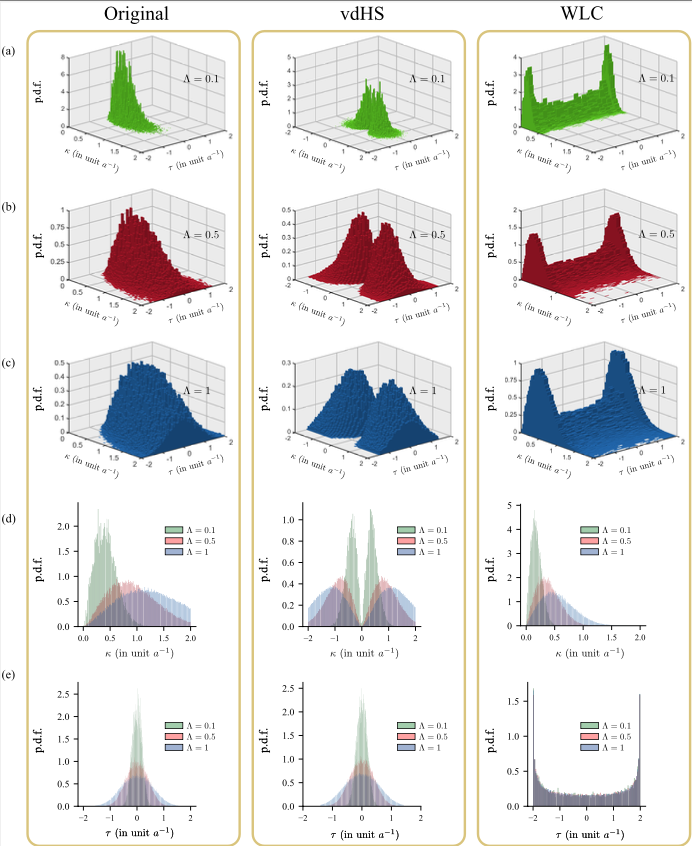
Ee Hou Yong, Farisan Dary, Luca Giomi, and L. Mahadevan,
“Reply to van der Heijden and Starostin: On the persistent helicity of fluctuating ribbons,”
Proceedings of the National Academy of Sciences of the United States of America, 121 (28), e2303436121, 2024.
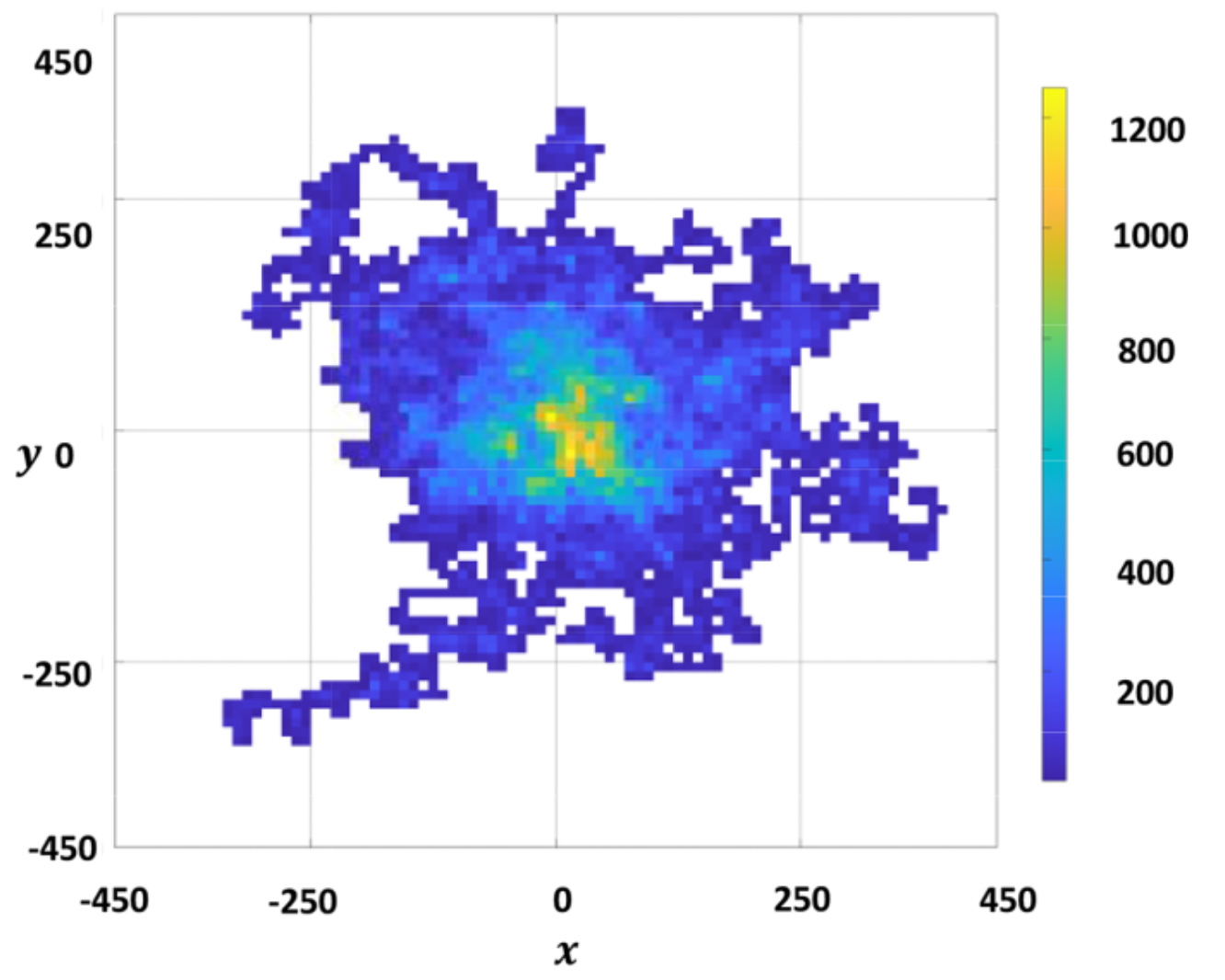
Nuoya Zhang and Ee Hou Yong,
“Dynamics, statistics, and task allocation of foraging ants,”
Physical Review E 108, 054306, 2023.
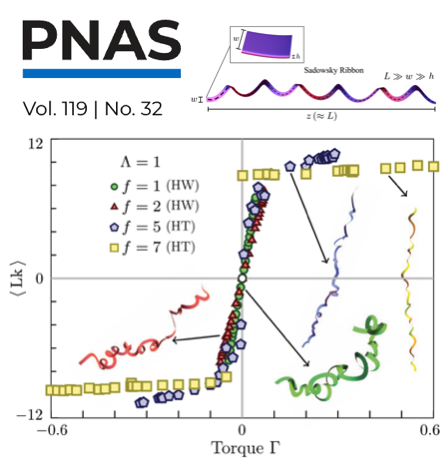
Ee Hou Yong, Farisan Dary, Luca Giomi, and L. Mahadevan,
"Statistics and topology of fluctuating ribbons,"

Mary Caswell Stoddard, Ee Hou Yong, Derya Akkaynak, Catherine Sheard, Joseph A. Tobias, and L. Mahadevan,
"Form, Function and Evolution of Avian Egg Shape,"
Science 356, 1249-1254, 2017.
Cover issue of vol. 356. Review Article on paper

Ee Hou Yong, David R. Nelson, and L. Mahadevan,
"Elastic Platonic Shells,"
Physical Review Letters 111(17), 177801, 2013.
Cover of Physical Review Letters vol. 111, issue 17
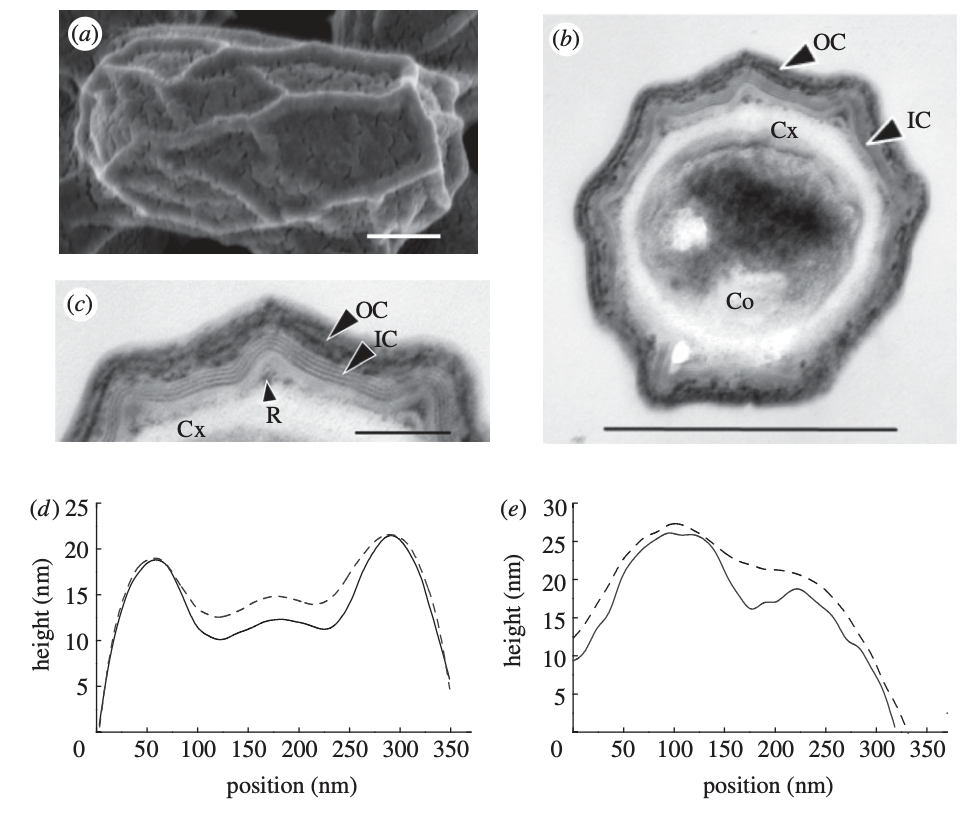
Ozgur Sahin, Ee Hou Yong, Adam Driks and L. Mahadevan,
"Physical basis for the adaptive flexibility of bacillus spore coats,"
Journal of the Royal Society Interface 9, 3156-3160, 2012.
