Statistical Physics
There is a growing literature of work that studies non-equilibrium processes in nature. Many powerful tools from statistical mechanics do not work for non-equilibrium systems where the traditional assumptions of thermal equilibrium and the thermodynamic limit no longer hold. Biological system is the archetypal non-equilibrium system: it consists of many individual units that can exchange energy, information, and matter continually with one another as well as the environment. My group has been working on the frontiers of non-equilibrium physics, such as overdamped Langevin dynamics, dynamically driven renormalization-group, Crooks fluctuation theorem, transport processes, control of complex network, etc. Some notable projects are listed below.
Shu Tian Eu and Ee Hou Yong,
"Contours information and the perception of various visual illusions,"
preprint on arXiv
Abstract: The simplicity principle states that the human visual system prefers the simplest interpretation. However, conventional coding models could not resolve the incompatibility between predictions from the global minimum principle and the local minimum principle. By quantitatively evaluating the total information content of all possible visual interpretations, we show that the perceived pattern is always the one with the simplest local completion as well as the least total surprisal globally, thus solving this apparent conundrum. Our proposed framework consist of (1) the information content of visual contours, (2) direction of visual contour, and (3) the von Mises distribution governing human visual expectation. We used it to explain the perception of prominent visual illusions such as Kanizsa triangle, Ehrenstein cross, and Rubin’s vase. This provides new insight into the celebrated simplicity principle and could serve as a fundamental explanation of the perception of illusory boundaries and the bi-stability of perceptual grouping.
Hong Chen and Ee Hou Yong,
"How zealots affect the energy cost for controlling complex social networks,"
Chaos 32, 063116, 2022.
Abstract: The controllability of complex networks may be applicable for understanding how to control a complex social network, where members share their opinions and influence one another. Previous works in this area have focused on controllability, energy cost, or optimization under the assumption that all nodes are compliant, passing on information neutrally without any preferences. However, the assumption on nodal neutrality should be reassessed, given that in networked social systems, some people may hold fast to their personal beliefs. By introducing some stubborn agents, or zealots, who hold steadfast to their beliefs and seek to influence others, the control energy is computed and compared against those without zealots. It was found that the presence of zealots alters the energy cost at a quadratic rate with respect to their own fixed beliefs. However, whether or not the zealots’ presence increases or decreases the energy cost is affected by the interplay between different parameters such as the zealots’ beliefs, number of drivers, final control time regimes, network effects, network dynamics, and number and configurations of neutral nodes influenced by the zealots. For example, when a network dynamics is linear but does not have conformity behavior, it could be possible for a contrarian zealot to assist in reducing control energy. With conformity behavior, a contrarian zealot always negatively affects network control by increasing energy cost. The results of this paper suggest caution when modeling real networked social systems with the controllability of networked linear dynamics since the system dynamical behavior is sensitive to parameter change.
Thomas H. Gray, Claudio Castelnovo, and Ee Hou Yong,
"Enhanced diffusion in soft-walled channels with a periodically varying curvature,"
Abstract: The motion of particles along channels of finite width is known to be hindered by either the presence of energy barriers along the channel direction or by variations in the width of the channel in the transverse direction (rugged channel). Remarkably, when both features are present, they can interact to produce a counterintuitive result: adding energy barriers to a rugged channel can enhance the rate of diffusion along it. This is the result of competing energetic and entropic effects. Under the approximation of particles instantaneously in equilibrium in the transverse direction, one can tailor the energy barriers to the ruggedness to recover free diffusion. However, such fine-tuning and potentially restrictive approximations are not necessary to observe an enhanced rate of diffusion as we demonstrate by adding a range of (non-fine-tuned) energy barriers to a channel of sinusoidally varying curvature. Furthermore, this was observed to hold for systems with a finite characteristic timescale for motion in the transverse direction, thus, suggesting that the phenomenon lends itself to be exploited for practical applications.
Hong Chen and Ee Hou Yong,
"Energy cost study for controlling complex social networks with conformity behavior,"
Physical Review E 104, 014301, 2021.
Abstract: In order to understand controlling a complex system, an estimation of the required effort needed to achieve control is vital. Previous works have addressed this issue by studying the scaling laws of energy cost in a general way with continuous-time linear dynamics. However, continuous-time linear dynamics is unable to capture conformity behavior, which is common in many complex social systems. Therefore, to understand controlling social systems with conformity, discrete-time modeling is used and the energy cost scaling laws are derived. The results are validated numerically with model and real networks. In addition, the energy costs needed for controlling systems with and without conformity are compared, and it was found that controlling networked systems with conformity features always requires less control energy. Finally, it is shown through simulations that heterogeneous scale-free networks are less controllable, requiring a higher number of minimum drivers. Since the conformity-based model relates to various complex systems, such as flocking, or evolutionary games, the results of this paper represent a step forward towards developing realistic control of complex social systems.
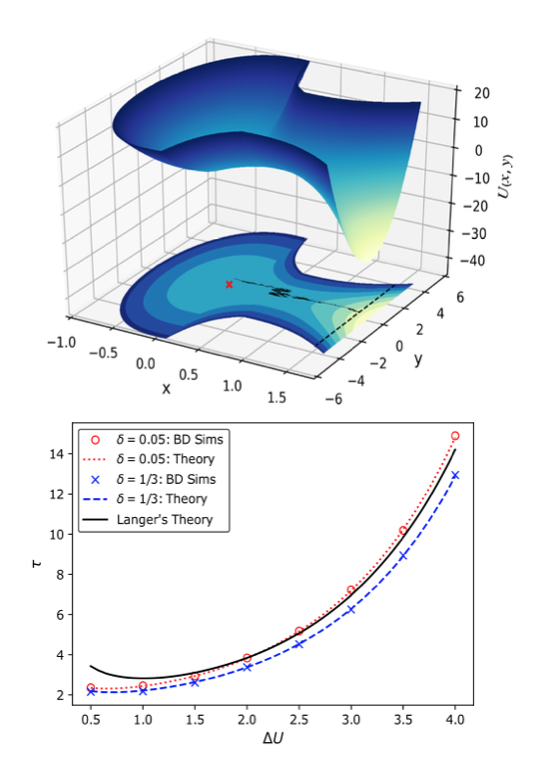
Thomas H. Gray and Ee Hou Yong,
"An effective one dimensional approach to calculating mean first passage time in multi-dimensional potentials,"
Journal of Chemical Physics 154, 084103, 2021.
Abstract: Thermally activated escape processes in multi-dimensional potentials are of interest to a variety of fields, so being able to calculate the rate of escape—or the mean first-passage time (MFPT)—is important. Unlike in one dimension, there is no general, exact formula for the MFPT. However, Langer’s formula, a multi-dimensional generalization of Kramers’s one-dimensional formula, provides an approximate result when the barrier to escape is large. Kramers’s and Langer’s formulas are related to one another by the potential of mean force (PMF): when calculated along a particular direction (the unstable mode at the saddle point) and substituted into Kramers’s formula, the result is Langer’s formula. We build on this result by using the PMF in the exact, one-dimensional expression for the MFPT. Our model offers better agreement with Brownian dynamics simulations than Langer’s formula, although discrepancies arise when the potential becomes less confining along the direction of escape. When the energy barrier is small our model offers significant improvements upon Langer’s theory. Finally, the optimal direction along which to evaluate the PMF no longer corresponds to the unstable mode at the saddle point.
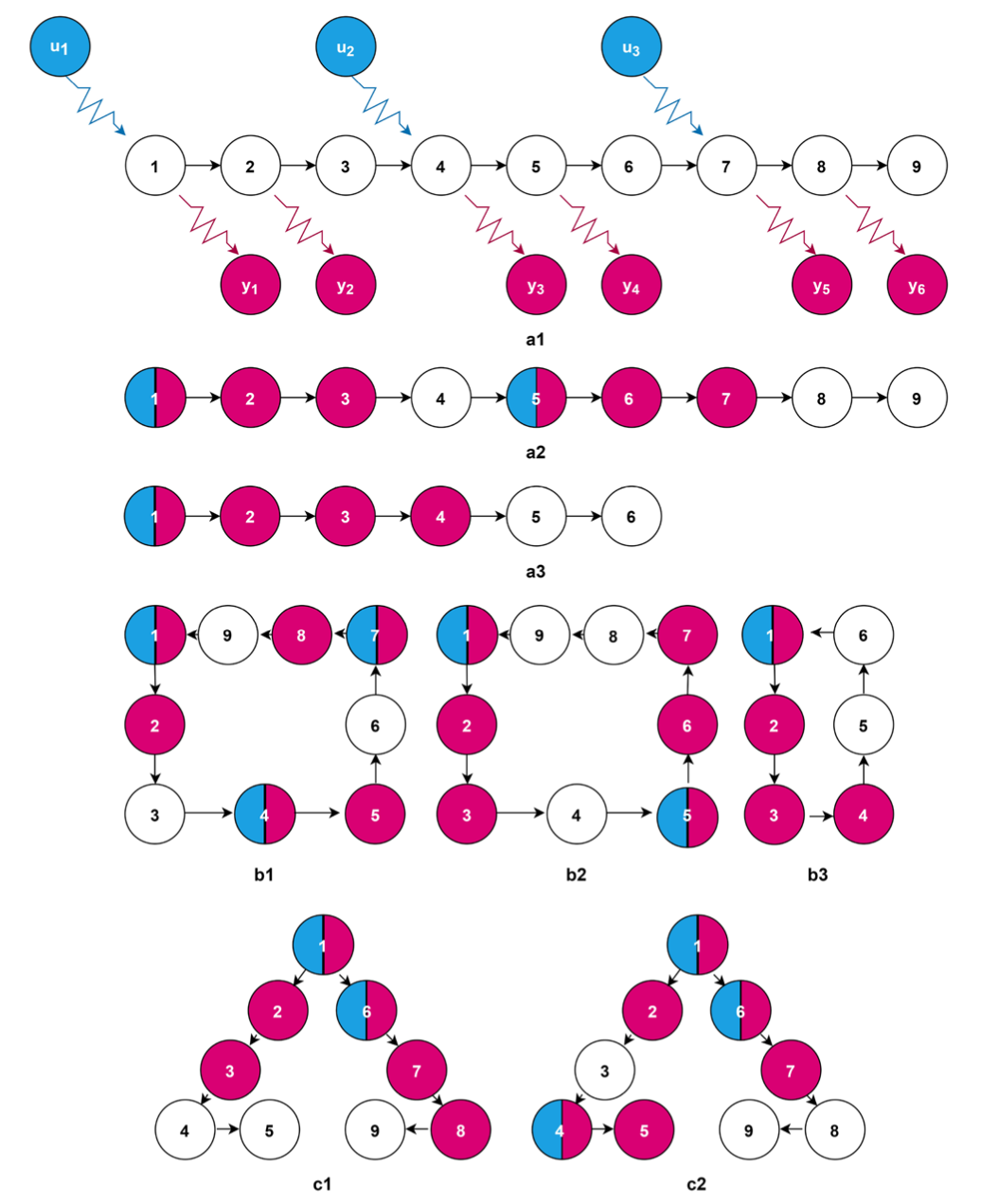
Hong Chen and Ee Hou Yong,
"Optimizing target node set for the control energy of directed complex networks,"
Scientific Reports 10, 18112, 2020.
Abstract: The energy needed in controlling a complex network is a problem of practical importance. Recent works have focused on the reduction of control energy either via strategic placement of driver nodes, or by decreasing the cardinality of nodes to be controlled. However, optimizing control energy with respect to target nodes selection has yet been considered. In this work, we propose an iterative method based on Stiefel manifold optimization of selectable target node matrix to reduce control energy. We derive the matrix derivative gradient needed for the search algorithm in a general way, and search for target nodes which result in reduced control energy, assuming that driver nodes placement is fixed. Our findings reveal that the control energy is optimal when the path distances from driver nodes to target nodes are minimized. We corroborate our algorithm with extensive simulations on elementary network topologies, random and scale-free networks, as well as various real networks. The simulation results show that the control energy found using our algorithm outperforms heuristic selection strategies for choosing target nodes by a few orders of magnitude. Our work may be applicable to opinion networks, where one is interested in identifying the optimal group of individuals that the driver nodes can influence.
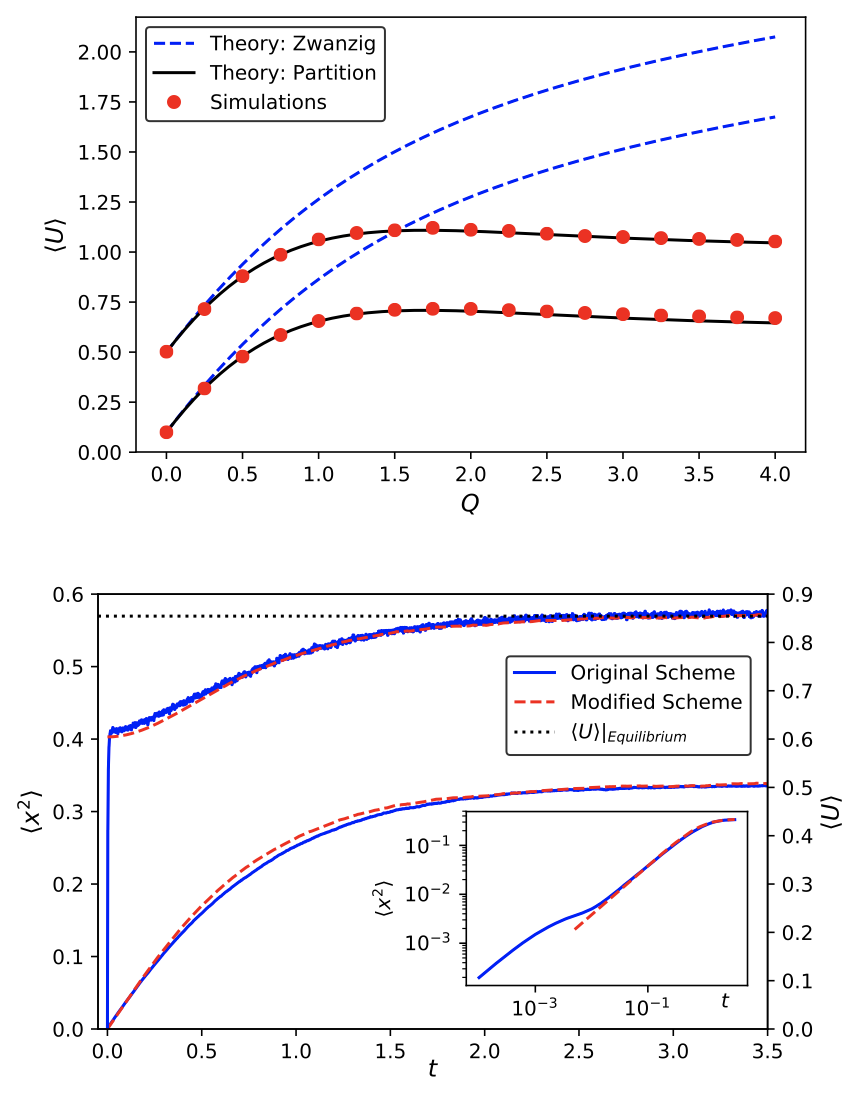
Thomas H. Gray and Ee Hou Yong,
"Effective diffusion in one-dimensional rough potential energy landscapes,"
Physical Review E 102, 022138, 2020.
Abstract: Diffusion in spatially rough, confining, one-dimensional continuous energy landscapes is treated using Zwanzig's proposal, which is based on the Smoluchowski Equation. We show that Zwanzig's conjecture only agrees with brownian dynamics simulations in the regime of small roughness. Our correction of Zwanzig's framework corroborates well with numerical results. A numerical simulation scheme based on our coarse-grained Langevin dynamics offers significant reductions in computational time. The mean first passage time problem in the case of random roughness is treated. Finally, we address the validity of separation of length scales assumption for the case of polynomial backgrounds and cosine-based roughness. Our results are applicable to hierarchical energy landscapes such as that of a protein’s folding, transport processes in disordered media, where there is clear separation of length scale between smooth underlying potential and its rough perturbation.
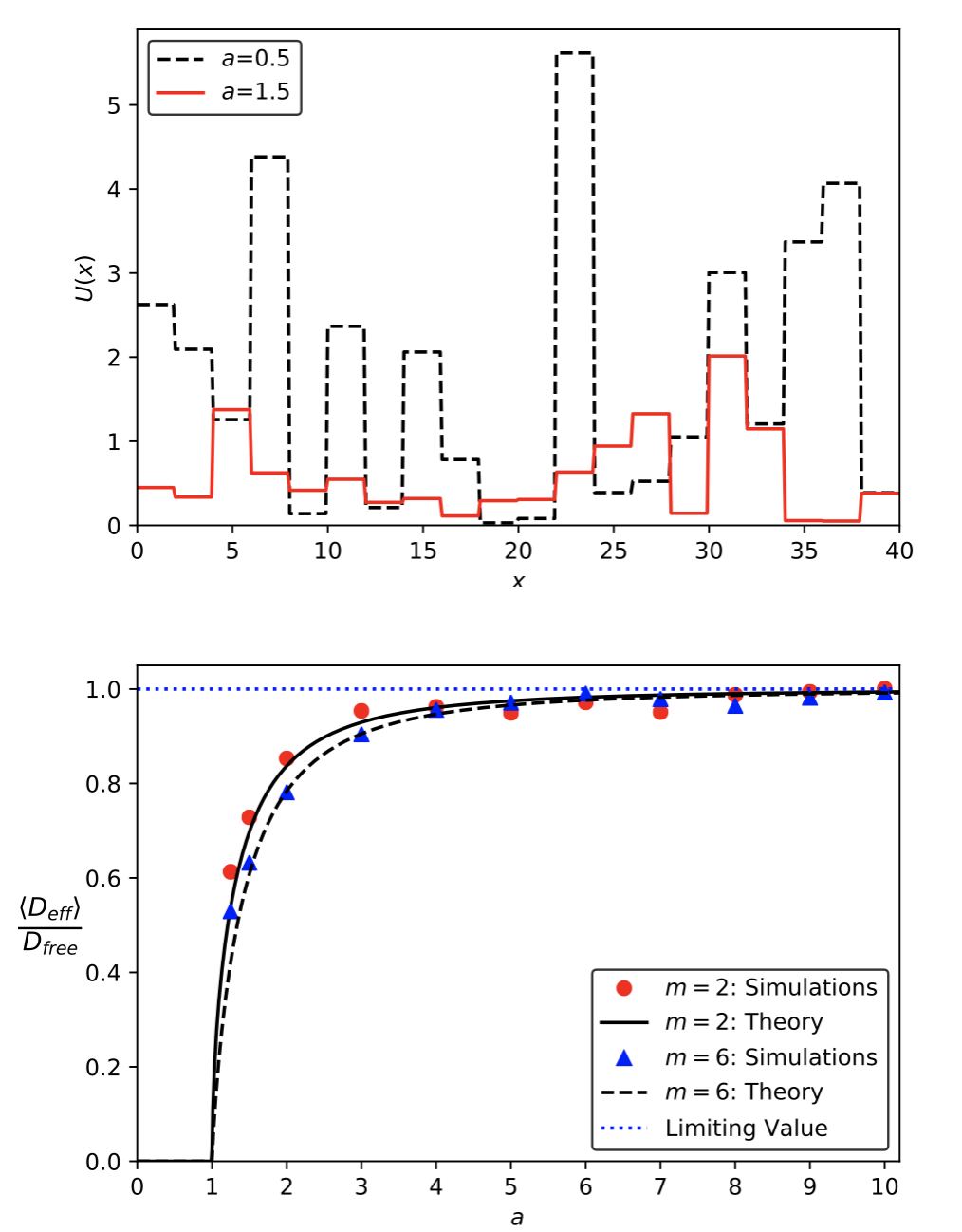
Thomas H. Gray and Ee Hou Yong,
"Overdamped Brownian dynamics in piecewise-defined energy landscapes,"
Physical Review E 101, 052123, 2020.
Abstract: We study the overdamped Brownian dynamics of particles moving in piecewise-defined potential energy landscapes U(x), where the height Q of each section is obtained from the exponential distribution p(Q) = aβexp(−aβQ), where β is the reciprocal thermal energy, and a > 0. The averaged effective diffusion coefficient ⟨Deff⟩ is introduced to characterize the diffusive motion: ⟨x^2⟩ = 2⟨Deff⟩t. A general expression for ⟨Deff⟩ in terms of U(x) and p(Q) is derived and then applied to three types of energy landscape: flat sections, smooth maxima, and sharp maxima. All three cases display a transition between sub-diffusive and diffusive behavior at a = 1, and a reduction to free diffusion as a → ∞. The behavior of ⟨Deff⟩ around the transition is investigated and found to depend heavily upon the shape of the maxima: Energy landscapes made up of flat sections or smooth maxima display power-law behavior, while for landscapes with sharp maxima, strongly divergent behavior is observed. Two aspects of the sub-diffusive regime are studied: the growth of the mean squared displacement with time and the distribution of mean first-passage times. For the former, agreement between Brownian dynamics simulations and a coarse-grained equivalent was observed, but the results deviated from the random barrier model’s predictions. The discrepancy could be a finite-time effect. For the latter, agreement between the characteristic exponent calculated numerically and that predicted by the random barrier model is observed in the large-amplitude limit.
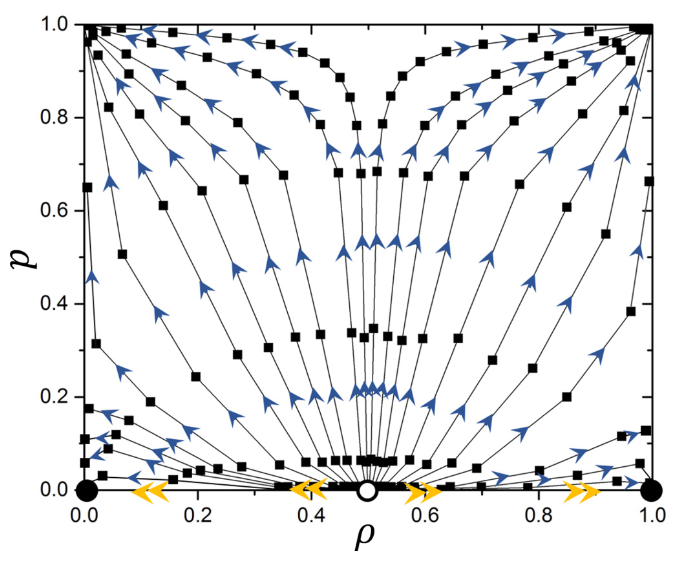
Han Kheng Teoh and Ee Hou Yong,
"Renormalization group study of Nagel-Schreckenberg model,"
Physical Review E 97, 032314, 2018.
Abstract: We study the phase transition from free flow to congested phases in the Nagel-Schreckenberg (NS) model by using the dynamically driven renormalization group (DDRG). The breaking probability p that governs the driving strategy is investigated. For the deterministic case p = 0, the dynamics remain invariant in each renormalization-group (RG) transformation. Two fully attractive fixed points, ρc∗ = 0 and 1, and one unstable fixed point, ρc∗ = 1/(vmax + 1), are obtained. The critical exponent ν which is related to the correlation length is calculated for various vmax. The critical exponent appears to decrease weakly with vmax from ν = 1.62 to the asymptotical value of 1.00. For the random case p > 0, the transition rules in the coarse-grained scale are found to be different from the NS specification. To have a qualitative understanding of the effect of stochasticity, the case p → 0 is studied with simulation, and the RG flow in the ρ−p plane is obtained. The fixed points p = 0 and 1 that govern the driving strategy of the NS model are found. A short discussion on the extension of the DDRG method to the NS model with the open-boundary condition is outlined.
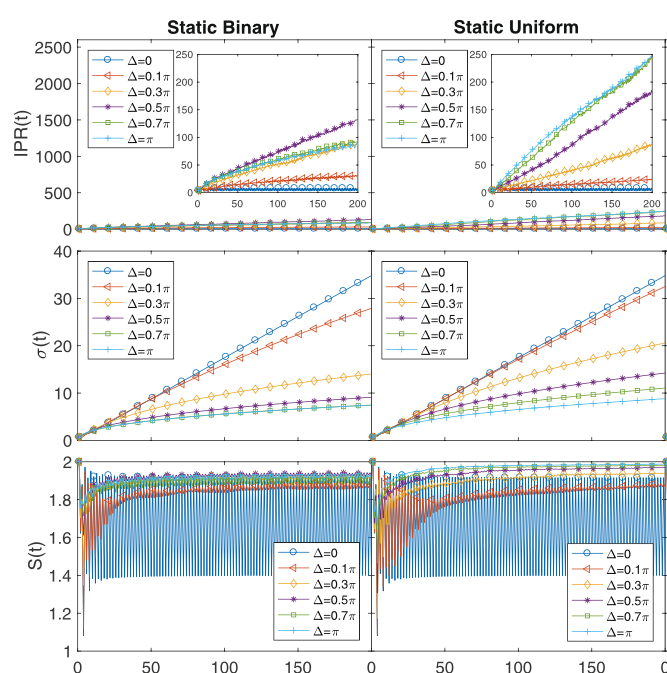
Meng Zeng and Ee Hou Yong,
"Discrete-Time Quantum Walk with Binary Phase Disorder: Localization and Entanglement Entropy,"
Scientific Reports 7, 12024, 2017.
Abstract: Quantum Walk (QW) has very different transport properties to its classical counterpart due to interference effects. Here we study the discrete-time quantum walk (DTQW) with on-site static/ dynamic phase disorder following either binary or uniform distribution in both one and two dimensions. For one dimension, we consider the Hadamard coin; for two dimensions, we consider either a 2-level Hadamard coin (Hadamard walk) or a 4-level Grover coin (Grover walk) for the rotation in coin-space. We study the transport properties e.g. inverse participation ratio (IPR) and the standard deviation of the density function (σ) as well as the coin-position entanglement entropy (EE), due to the two types of phase disorders and the two types of coins. Our numerical simulations show that the dimensionality, the type of coins, and whether the disorder is static or dynamic play a pivotal role and lead to interesting behaviors of the DTQW. The distribution of the phase disorder has very minor effects on the quantum walk.
Meng Zeng and Ee Hou Yong,
"Crooks Fluctuation Theorem in PT-symmetric Quantum Mechanics,"
Journal of Physics Communications 1, 031001, 2017.
Abstract: Following the recent work by Deffner and Saxena (2015 Phys. Rev. Lett. 114 150601), where the Jarzynski equality is generalised to non-Hermitian quantum mechanics, we prove in this work a stronger form of Jarzynski equality, the Crooks fluctuation theorem, also in the non-Hermitian formalism when the system is in the unbroken -symmetric phase.
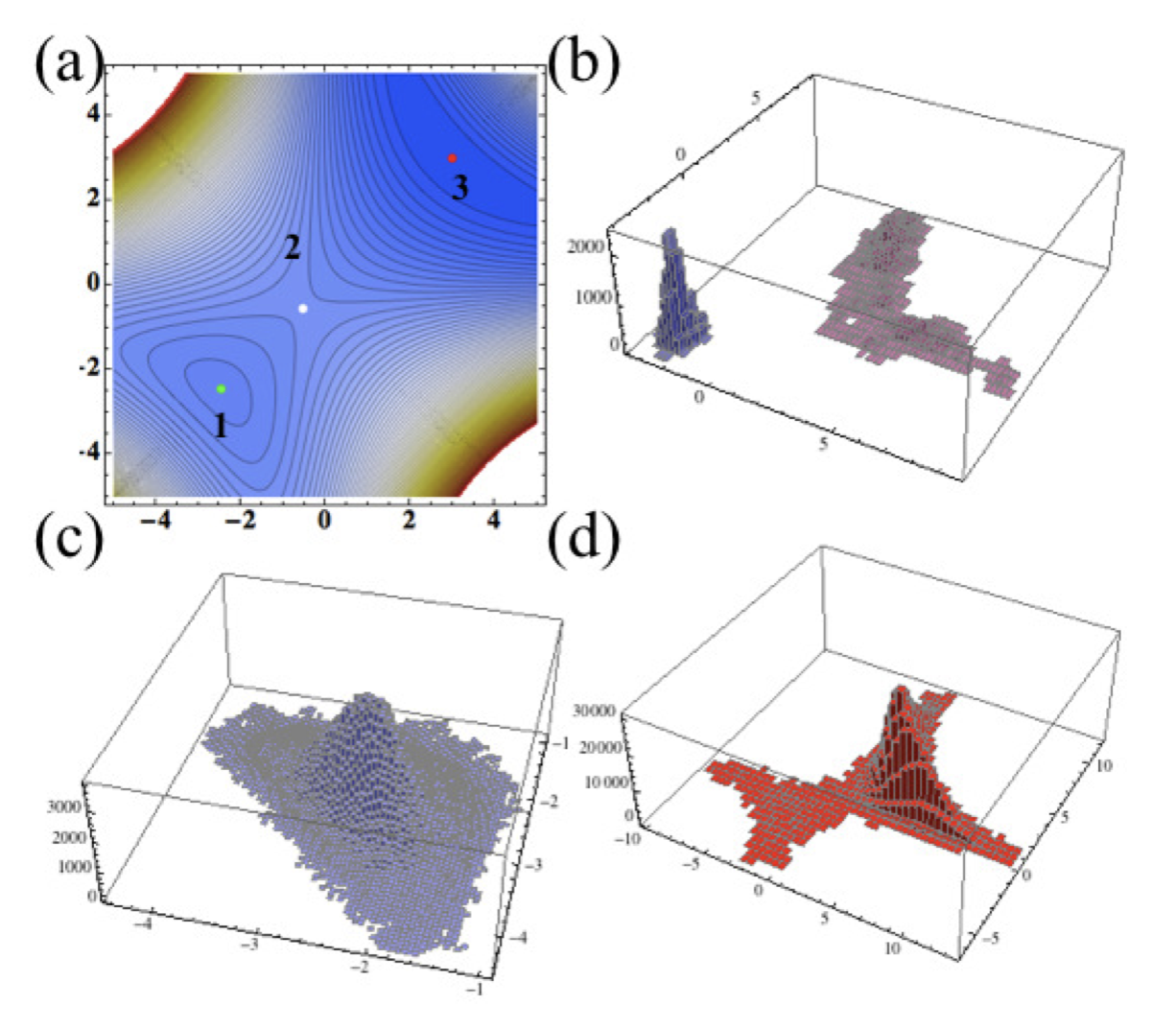
Ee Hou Yong, and L. Mahadevan,
"Statistical Mechanics and Shape Transitions in Microscopic Plates,"
Physical Review Letters 112, 048101, 2014.
Abstract: Unlike macroscopic multistable mechanical systems such as snap bracelets or elastic shells that must be physically manipulated into various conformations, microscopic systems can undergo spontaneous conformation switching between multistable states due to thermal fluctuations. Here we investigate the statistical mechanics of shape transitions in small elastic elliptical plates and shells driven by noise. By assuming that the effects of edges are small, which we justify exactly for plates and shells with a lenticular section, we decompose the shapes into a few geometric modes whose dynamics are easy to follow. We use Monte Carlo simulations to characterize the shape transitions between conformational minimal as a function of noise strength, and corroborate our results using a Fokker-Planck formalism to study the stationary distribution and the mean first passage time problem. Our results are applicable to objects such as graphene flakes or protein β sheets, where fluctuations, geometry, and finite size effects are important.
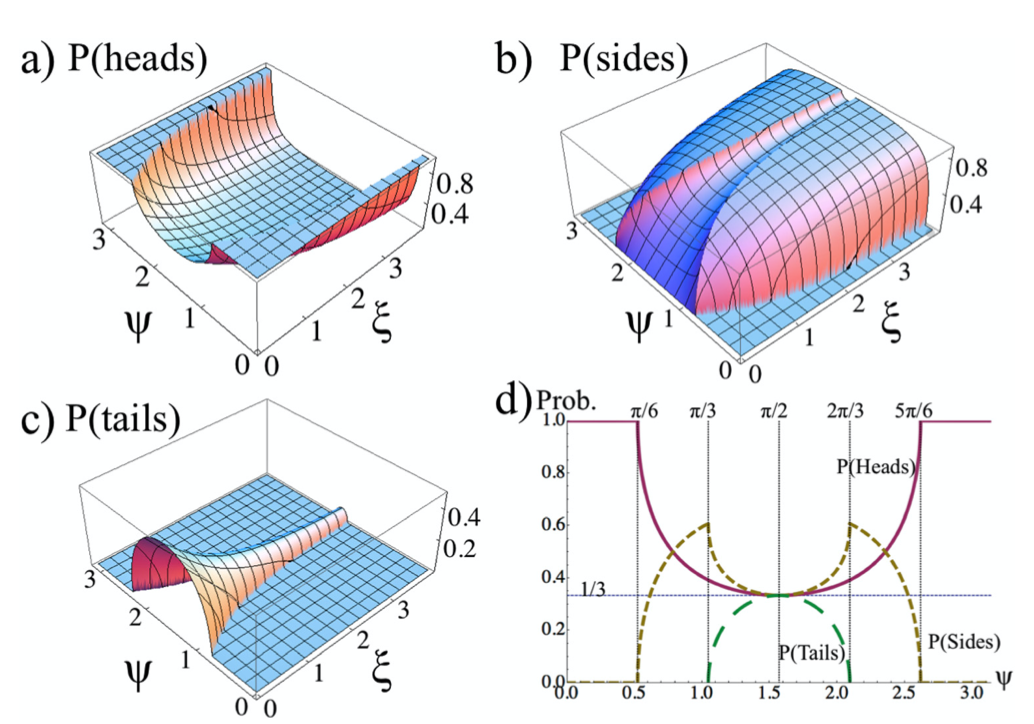
Ee Hou Yong and L. Mahadevan,
"Probability, geometry and dynamics in the toss of a thick coin,"
American Journal of Physics 79(12):1195-1201, 2011.
Cover of American Journal of Physics vol. 79, issue 12
Abstract: When a thick cylindrical coin is tossed in the air and lands without bouncing on an inelastic substrate, it ends up on its face or its side. We account for the rigid body dynamics of spin and precession and calculate the probability distribution of heads, tails, and sides for a thick coin as a function of its dimensions and the distribution of its initial conditions. Our theory yields a simple expression for the aspect ratio of homogeneous coins with a prescribed frequency of heads or tails compared to sides, which we validate using data from the results of tossing coins of different aspect ratios.